Miért van a valami, a semmi helyett? Hogyan jöhetett létre a semmiből valami?

A felületes szemlélő mostanában azt hihetné Boniról, hogy tipikusan „kocka”, akit a matek meg a fizika érdekli. Ezt a véleményét abból vezetné le, hogy Boni folyton számol(gat), mostanában például a Pitagorasz-tételt ellenőrzi, illetve fizikakönyveket tanulmányoz, jegyzetel (ír!) és az egyik kedvenc társasjátéka a Turing Machine.

Pedig én jól tudom, hogy még ezekben a tevékenységeiben is ő egy valódi bölcsész és filozófus, akit valójában az bűvöl el, hogy a számokat, azaz a méretet, a távolságot, a nagyságot stb., vagy azok hiányát, jelekkel le lehet írni. Hogy vannak olyan, a szavaknál is megfoghatatlanabb jelenségek, amelyeket szintén rögzíteni lehet papíron, és hogy ehhez külön rendszert kellett, önkényesen ráadásul, kitalálni, azaz a számrendszert!

Egyik mesekönyve például valahogy így kezdődött: az ősrobbanás után létrejött a tér és az idő. Hát nem őrület?! A végtelen fogalmával együtt? Hogy az örökkéről már ne is beszéljünk?! Vagy hogy a Nap körül keringő égitesteket olyan köznapi jelenségekkel lehet megmagyarázni, mint egy alma lepottyanása a fáról! De a kvantumfizika ugyanígy lenyűgözi, érthető módon: hogy a fénysebességnél is lehet gyorsabb! Ráadásul egy időben lenni két helyen!

Ezek mind olyan matekos ügyek, amelyek rokonok a filozófiával. A valószínűségszámítás szintén. Hogyan van az például, hogy ha elgurítunk egy kockát, annak az eredménye lehet egyszerre előre determinált (hiszen ha nagyon sokszor dobjuk el, az 1–6 számok hasonló arányban jönnek ki) ugyanakkor probabilista is (mert ha egyszer dobjuk el, megjósolhatatlan, hogy mit kapunk). Vagy: van-e az univerzumban véletlen?

Elmeséltem neki a Monty-Hall paradoxont. Ez egy olyan feladvány, amelyteljesen szembe megy a józan paraszti ésszel, ugyanakkor gyorsan levezethető papíron, és utána könnyű átlátni és megérteni (elhinni viszont nem). Röviden: egy játékosnak választania kell három zárt ajtó közül. Az egyik mögött egy autó van, a másik kettő mögött egy-egy kecske. Miután kiválasztott egy ajtót (legyen ez az 1. ajtó) a műsorvezető megmutatja, hogy a fennmaradó két ajtó közül melyik mögött van kecske (a példában mondjuk a 2. ajtó) és megkérdezi tőle, hogy szeretné-e módosítani eredeti választását (azaz inkább a 3. ajtót választani) vagy megmarad az 1. ajtónál? 

Tehát az a kérdés, hogy a játékos növeli-e az esélyét az autóra, ha a plusz infó birtokában eláll az eredeti döntésétől. A válasz: igen. Ha a játékos megváltoztatja eredeti döntését, nagyobb esélye van arra, hogy megnyeri az autót. Első látásra nem logikus, miért kellene módosítania? Hiszen most két ajtó van előtte, egyik mögött egy kecske, másik mögött egy autó, de még mindig nem tudja melyik mögött mi van. Akkor miért változtasson?

Én ezt akkor értettem meg, amikor felvázoltam a lehetséges opciókat. Vegyünk pl. egy olyan helyezetet, amikor az ajtók mögött ez van:

1. ajtó: autó (A)

2. ajtó: kecske (K)

3. ajtó: kecske (K)

Ez csak egyetlen lehetőség a három közül (az autó lehet a 2. és a 3. ajtó mögött is), de a többi ugyanígy lezongorázható, ezért azokat nem veszem sorra. A játékosnak ebben az esetben ezek a döntési lehetőségei vannak:

Döntési lehetőségek

 

Ez azt jelenti, hogy 1/3-ad esélye van arra, hogy véletlenszerűen a kocsit válassza:

A háromból egyszer (1/3) lesz övé az autó

 

Ez történik akkor, ha az eredeti döntését a játékos később nem módosítja. Eddig ez logikus és egyértelmű. Miután azonban a műsorvezető megmutatta a játékosnak, hogy a fennmaradó két ajtó közül melyik mögött van kecske (az első két variációban a 3. ajtó, az utolsó variációban a 2. ajtó mögött), és a játékos megváltoztatja a döntését (sárga nyilak), abban az esetben, mint ahogy a táblázatból kiderül, háromból kétszer megnyeri az autót:

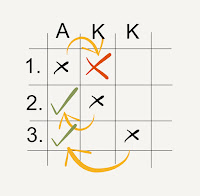A háromból kétszer (2/3) lesz övé az autó

 

(Ehhez hasonló feladvány: egy embernek két gyereke van. Az egyik lány. Mennyi az esélye annak, hogy a másik fiú? Ki tudja levezetni?)